# theory

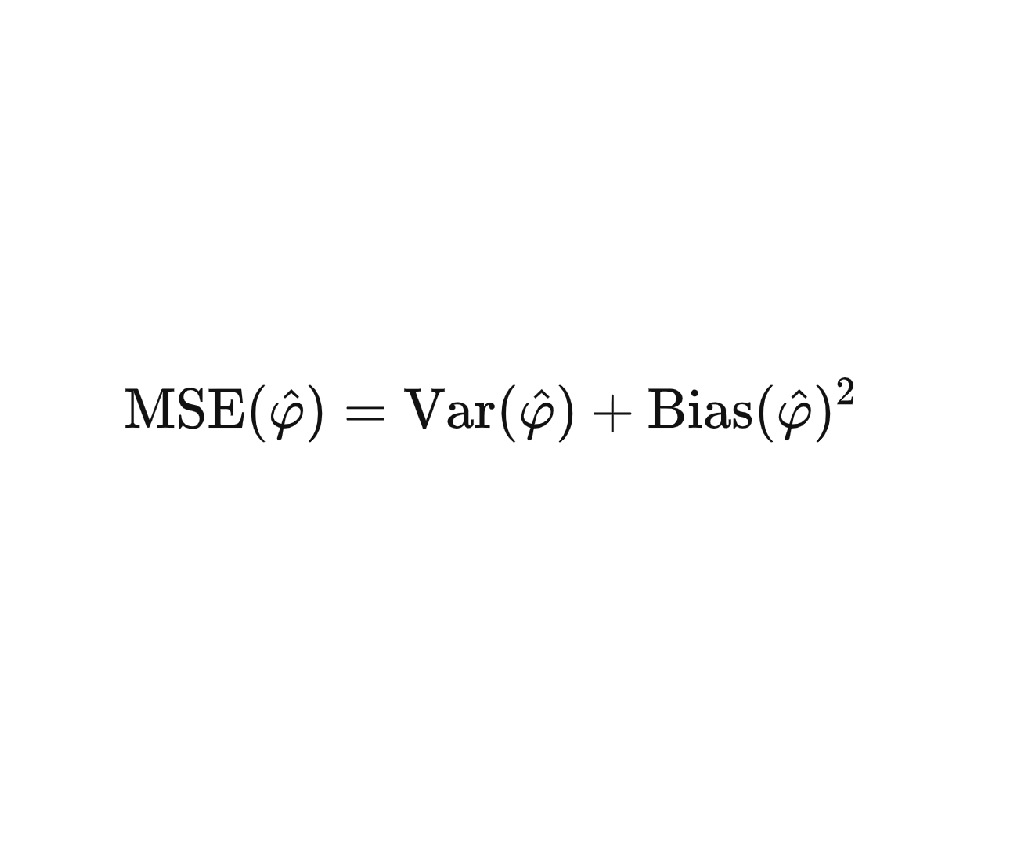
The bias-variance decomposition allows one to decompose the contributions to the mean-squared error of an estimator into two parts, the variance stemming from the fluctuations of the prediction and the bias measuring the deviation of the expected value of the prediction from the true value. While being a very straightforward relation, it allows fundamental insight into necessary tradeoffs when constructing estimators. In this post I show how to derive the bias-variance decomposition in the multivariate setting motivated by a use case in quantum metrology and talk a bit about Stein’s paradox.

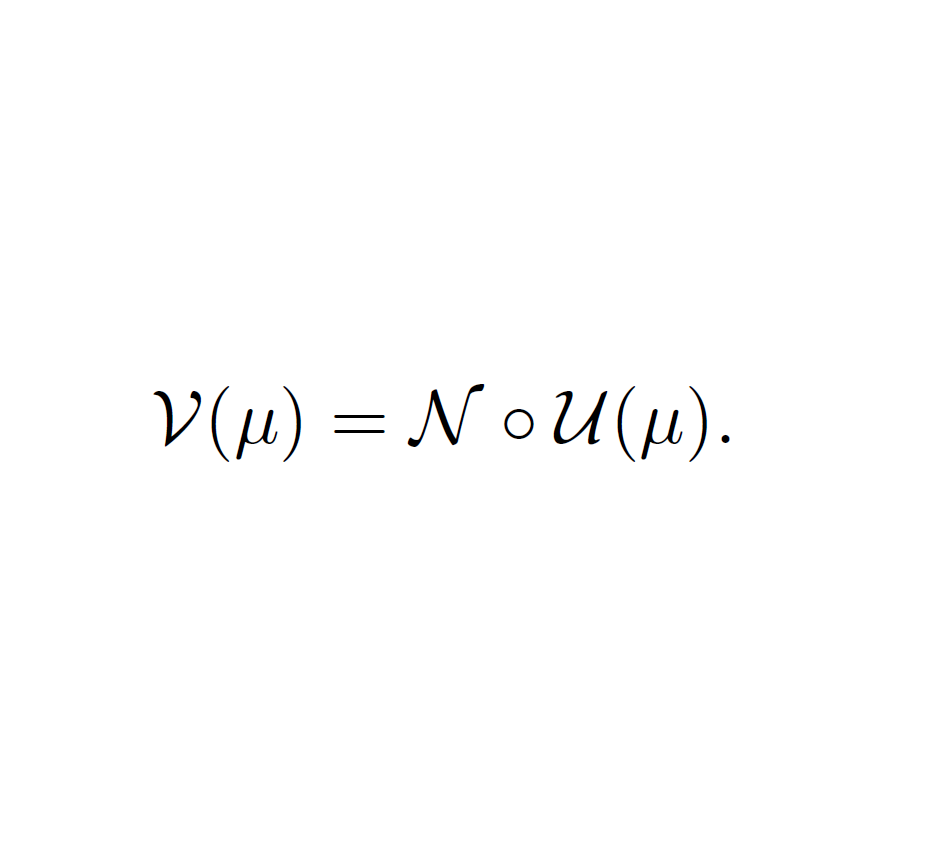
The parameter-shift rule is a workhorse for the optimization of parametrized quantum circuits. In this post, I explain how it also works in a noisy context and how we can extend it to convex combinations of quantum channels. This blog post is a summary of Appendix A of our paper A variational toolbox for quantum multi-parameter estimation ¹.